 2014-09-15 14:11:50 ใน ความรู้ทั่วไป »
2014-09-15 14:11:50 ใน ความรู้ทั่วไป »  0
0  20739
20739 ความรู้พื้นฐานด้านดิจิตอล (Number System)
การแทนที่สภาวะของกระแสไฟฟ้าได้ 2 สภาวะ คือ สภาวะที่มีกระแสไฟฟ้า และสภาวะที่ไม่มีกระแสไฟฟ้า และเพื่อให้โปรแกรมเมอร์สามารถสั่งการคอมพิวเตอร์ได้ จึงได้มีการสร้างระบบตัวเลขที่นำมาแทนสภาวะของกระแสไฟฟ้า โดย ตัวเลข 0 จะแทนสภาวะไม่มีกระแสไฟฟ้า หรือ ปิด (off) เลข 1 แทนสภาวะมีกระแสไฟฟ้า หรือเปิด (on)
จึงได้กำหนดตัวเลขที่มีจำนวน 2 จำนวน (2 ค่า) เรียกว่าระบบเลขฐานสอง (Binary Number System) ซึ่งเป็นระบบตัวเลขที่สามารถนำมาใช้ในการสั่งงานคอมพิวเตอร์ โดยการแทนที่สภาวะต่างๆ ของกระแสไฟฟ้า แต่ในชีวิตประจำวันของคนเราจะคุ้นเคยกับตัวเลขที่มีจำนวน 10 จำนวน คือ เลข 0 - 9 ซึ่งเรียกว่าระบบเลขฐานสิบ (Decimal Number System) ดังนั้นจึงมีความจำเป็นต้องศึกษาระบบเลขฐาน ประกอบการศึกษาวิชาด้านคอมพิวเตอร์ เพื่อความเข้าใจพื้นฐานการทำงานของเครื่องคอมพิวเตอร์ สำหรับการประยุกต์ใช้งานกับ PLC ในที่นี้จะกล่าวถึงเพียงเเค่ ระบบเลขฐานสอง,สิบ,สิบหกเท่านั้น
ระบบเลขฐานสอง (Binary) ประกอบด้วยตัวเลข 0 และ 1
ระบบเลขฐานสิบ (Decimal) ประกอบด้วยตัวเลข 0 - 9
ระบบเลขฐานสิบหก (Hexadecimal) ประกอบด้วยตัว เลข 0 - 9 และ A - F
ความสัมพันธ์ของเลข BIN, BCD และ HEX สามารถกำหนดให้เป็นตารางได้ดังนี้
|
HEX
|
BCD
|
FOUR DIGIT BINARY
|
|
|
|
2^3 = 8
|
2^2 = 4
|
2^1 = 2
|
2^0 = 1
|
|
0
|
0
|
0
|
0
|
0
|
0
|
|
1
|
1
|
0
|
0
|
0
|
1
|
|
2
|
2
|
0
|
0
|
1
|
0
|
|
3
|
3
|
0
|
0
|
1
|
1
|
|
4
|
4
|
0
|
1
|
0
|
0
|
|
5
|
5
|
0
|
1
|
0
|
1
|
|
6
|
6
|
0
|
1
|
1
|
0
|
|
7
|
7
|
0
|
1
|
1
|
1
|
|
8
|
8
|
1
|
0
|
0
|
0
|
|
9
|
9
|
1
|
0
|
0
|
1
|
|
A
|
-
|
1
|
0
|
1
|
0
|
|
B
|
-
|
1
|
0
|
1
|
1
|
|
C
|
-
|
1
|
1
|
0
|
0
|
|
D
|
-
|
1
|
1
|
0
|
1
|
|
E
|
-
|
1
|
1
|
1
|
0
|
|
F
|
-
|
1
|
1
|
1
|
1
|
BIN (Binary) = ระบบเลขฐานสอง
BCD (Binary Code Decimal) = ระบบเลขฐานสิบ
HEX (Hexadecimal) = ระบบเลขฐานสิบหก
1. ระบบเลขฐานสอง (Binary)
ระบบเลขฐานสอง (Binary) - ระบบเลขฐานสอง จะใช้อักขระแทนสองตัว เเละเนื่องจากระบบเลขฐานสองนี้ใช้ในระบบดิจิตอลอิเล็กทรอนิกส์ด้วย เพราะว่าวงจรดิจิตอลจะมีเพียงสองสถานะ(two states)หรือระดับสัญญาณสองระดับ (two signal levels)โดยมีตัวเลขที่ไม่ซ้ำกันอยู่ทั้งหมด 2 ตัว คือ 0 และ 1 หรืออาจใช้คำอื่นแทน
|
สถานะหนึ่ง
|
สถานะตรงข้าม
|
|
0
|
1
|
|
Off
|
On
|
|
Space
|
Mark
|
|
Open
|
Closed
|
|
Low
|
Hi
|
เลขฐานสองจะมีจำนวนหลักมากกว่าเลขฐานสิบ เพราะว่าในแต่ละหลักจะมีเลขได้สองค่า แต่ถ้าเป็นเลขฐานสิบแต่ละหลักจะมีเลขได้เก้าค่าคือ 0 ถึง 9
ระบบเลขฐานสิบ แต่ละหลักจะมีค่าเวจต์เป็นค่าสิบยกกำลังของหลักนั้น ระบบเลขฐานสองก็เช่นเดียวกัน จะมีฐานของเลขฐานสอง (base 2 system) การหาค่าเวจต์ในแต่ละหลักจะหาได้จากค่ายกกำลังสองของหลักนั้นๆ
|
ฐานสอง
|
ฐานสิบ
|
|
2^0
|
1
|
|
2^1
|
2
|
|
2^2
|
4
|
|
2^3
|
8
|
|
2^4
|
16
|
|
2^5
|
32
|
|
2^6
|
64
|
|
2^7
|
128
|
|
2^8
|
256
|
|
2^9
|
512
|
|
2^10
|
1024
|
ค่าของ2ยกกำลังต่างๆเป็นฐานสิบ
ถ้าต้องการแปลงเลขฐานสองเป็นเลขฐานสิบก็สามารถทำได้ เช่นถ้าแปลงเลข 101101 เป็นเลขฐานสิบสามารถทำได้ดังนี้
(1x2^5)+(0x2^4)+(1x2^3)+(1x2^2)+(0x2^1)+(1x2^0) = 45
ตัวเลขฐานสอง 101101 จะมีค่าเท่ากับ 45 ในระบบเลขฐานสิบ
ระบบเลขฐานสองก็มีทศนิยมเช่นเดียวกับระบบเลขฐานสิบ ซึ่งเรียกว่าไบนารีพอยต์(binary point) โดยจะมีเครื่องหมายจุดแบ่งตัวเลขจำนวนเต็มกับเลขทศนิยมออกจากกัน ค่าเวจต์ของเลขทศนิยมแต่ละหลักจากซายไปขวาจะเป็นดังนี้ 1/2 , 1/4 , 1/8 , 1/16........ไปเรื่อยๆหรืออาจจะเขียนเป็นเลขยกกำลังค่าลบก็ได้
|
ฐานสอง
|
ฐานสิบ
|
|
2^ -1
|
0.5
|
|
2^ -2
|
0.25
|
|
2^ -3
|
0.125
|
|
2^ -4
|
0.0652
|
|
2^ -5
|
0.03125
|
|
2^ -6
|
0.015625
|
ค่าของ2ยกกำลังค่าลบ เป็นเลขฐานสิบ
ในระบบเลขฐานสิบนั้นแต่ละหลักจะเรียกว่าหลัก แต่ถ้่าเป็นระบบเลขฐานสองแต่ละหลักจะเรียกว่าบิต (bit) คำว่าบิต (bit) ย่อมาจาก binary digit ถ้าในงานดิจิตอลอิเล็กทรอนิกส์ จะพบคำว่า “Bit” บ่อยมาก
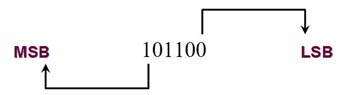
ในแต่ละหลักของเลขฐานสอง หลักซึ่งมีค่าเวจต์ต่ำสุดซึ่งอยู่ทางด้านขวาสุด จะเรียกว่าบิตที่มีความสำคัญต่ำสุด(LSB : Least Significant Bit) สำหรับด้านที่อยู่ซ้ายสุดจะมีค่าเวจต์สูงสุด เรียกว่าบิตที่มีความสำคัญสูงสุด(MSB : Most Significant Bit) ถ้าใช้ในระบบเลขฐานสิบจะเรียกว่า LSD(Least Significant Digit) และ MSD(Most Significant Digit) ในระบบดิจิตอลในบางครั้งเราจะเห็นเขียนว่า MSD , LSD กำกับเอาไว้ด้วย
2. ระบบเลขฐานสิบ (Decimal)
ระบบเลขฐานสิบ (Decimal) มีตัวเลขที่ไม่ซ้ำกันอยู่ทั้งหมด 10 ตัว คือ 0 1 2 3 4 5 6 7 8 9 หรือเรียกอีกอย่างหนึ่งคือ BCD code อันนี้คงไม่ต้องกล่าวอะไรมากเพราะอยู่ใ้นชีวิตประจำวันอยู่แล้ว
3. ระบบเลขฐานสิบหก (Hexadecimal)
ระบบเลขฐานสิบหก (Hexadecimal) ฐานของมันจะมีค่าเป็น 16 ซึ่งจะมีตัวเลขที่ไม่ซ้ำกันอยู่ทั้งหมด 16 ตัว คือ 0 1 2 3 4 5 6 7 8 9 A B C D E F (ตัวอักษร 6 ตัว แทน ตัวเลข 10 –15 ตามลำดับ)
ในงานด้านอิเล็กทรอนิกส์และคอมพิวเตอร์ ตัวเลขที่ใช้ในการประมวลผลจะเป็นเลขฐานสอง แต่ถ้าตัวเลขมีค่ามากจะทำให้เลขฐานสองมีหลายหลัก จึงใช้เลขฐานสิบหกแทนเลขฐานสอง แล้วจะมีการแปลงเลขฐานสิบหกเป็นเลขฐานสองอีกทีหนึ่ง เลขฐานสิบหกนั้นจะนิยมใช้มากในคอมพิวเตอร์ ถ้าหากไบนารี่ที่ใ่ช้ในระบบคอมพิวเตอร์เป็นแบบ 8 บิต ซึ่งแทนเลขฐานสิบหกได้ตั้งเเต่ 0 ถึง 255 แต่สามารถแทนด้วยเลขฐานสิบหกเพียงสองหลักเท่านั้น ถ้าหากเรามีเลขฐานสิบ 99,999,999 ถ้าเขียนแทนด้วยเลขไบนารีจะต้องใช้หลายบิต แต่ถ้าเขียนเเทนด้วยเลขฐานสิบหกจะใช้เพียงไม่กี่หลัก
ค่าสิบหกสามารถแทนได้ด้วยสองยกกำลังสี่ หรือ 16 = 2^4 ดังนั้นเลขฐานสิบหกจึงสามารถเขียนแทนด้วยเลขฐานสองได้สี่บิต โดยมีค่าตั้งแต่ 0000 ถึง 1111 หรือแทนด้วยอักษร 0 ถึง F ความสัมพันธ์ระหว่างเลขฐานสอง ฐานสิบ และฐานสิบหกแสดงใ้ว้ในตารางความสัมพันธ์ของเลข BIN, BCD และ HEX
การแปลงเลขฐานสองเป็นเลขฐานสิบหกก็สามารถทำได้โดยง่าย โดยจัดเลขฐานสองตั้งแต่บิตแรกจนถึงบิตสุืดท้ายเป็นกลุ่มๆ โดยจัดกลุ่มละ 4 บิตและแทนค่าด้วยเลขฐานสิบหกแต่ละค่าให้สอดคล้องกันตัวอย่างต่อไปนี้จะเป็นการแปลงเลขฐานสองเป็นฐานสิบหก
การแปลงเลข 10101011111101 เป็นเลขฐานสิบหกสามารถทำได้โดย การแบ่งกลุ่ม ๆ ละ 4 บิตดังนี้
0010 1010 1111 1101
จะเห็นว่าถ้าแบ่งเป็นกลุ่ม ๆ ละ 4 บิต จะมีสองบิตบนที่จัดกลุ่มไม่ได้ ก็ให้เติม 0 ไปในกลุ่มนั้นให้ครบ 4 บิต จากนั้นแทนค่าตัวเลขแต่ละกลุ่มด้วยเลขฐานสิบหกดังนี้
2 A F D
ดังนั้นจะได้ 10101011111101 มีค่าเท่ากับ 2AFD
ให้จำใว้ว่าเลขฐานสิบหกที่เรามองเห็นนั้นเป็นการใช้แทนเลขไบนารีเพราะ CPU ไม่สามารถประมวลผลเลขฐานสิบหกได้
ประเภทของข้อมูลเช่น บิต, ไบต์, เวิร์ด
ข้อมูลภายใน PLC จะมีคำจำกัดความที่เรียกกันคือ บิต (BIT), ไบต์ (Byte), เวิร์ด (Word) หลักการเรียกและความหมายของแต่ละคำมีดังนี้
1 Word = 2 Byte
1 Byte = 2 Digit
1 Digit = 4Bit
เช่น ข้อมูลขนาด 256 กิโลบิต (kBit) จะสามารถเก็บข้อมูลได้กี่กิโลไบต์ ?
8 บิต = 1 ไบต์
256 กิโลบิต = (256 x 1000)/8 = 32,000 ไบต์
= 32 กิโลไบต์
หน่วยความจำ ขนาด 6 kWords ถ้าจะเปลี่ยนหน่วยเป็น kB. จะได้เท่าไร ?
1 Word = 2 ไบต์
6 kWord = 2 x 6 x 1000 = 12,000 ไบต์
= 12 กิโลไบต์
ขอขอบคุณ
www.star-circuit.com
www.pccpl.ac.th

